TEKNIK MESIN 45-NABHAN: Integral

Integral

Setelah kemaren dipuyengkan tentang perhitungan statistik kini dosen kalkulus kebanggaan kita masuk ke teknik integral, yupsssss.....benar sekali alangkah baiknya, kita sharing sama-sama menguak habis misteri dibalik integral.....sebenarnya pembahasan ini udah dibab sebelumnya kita bahas ya....waktu menghitung volume benda tak tentu menggunakan teknk pengintegralan juga kan.....
kita harus bisa itu intinya.....

Integral merupakan kebalikan dari turunan.

Jika suatu fungsi f (x) mempunyai turunan f ' (x) maka turunan tersebut bila diintegralkan akan diperoleh kembali fungsi f (x). Penulisan lambang integralnya sebagai berikut :

Sebagai contoh :

Suatu fungsi f (x) = 5x³ + 4x² - 3x + 7 tentukanlah turunan fungsi f (x) tersebut...?

f ' (x) = 15x² + 8x - 3

Untuk memperoleh kembali fungsi f (x) dari turunannya yaitu f ' (x) maka kita perlu mengintegralkan turunannya tersebut :

Sebelumnya...
kita perlu mengenal terlebih dahulu rumus dasar integral untuk fungsi f (x)

f (x) = xⁿ maka integral dari f (x) :

Kembali lagi ke soal sebelumnya....

Jika f ' (x) = 15x² + 8x - 3 maka f(x) =....?

Jawab :

f (x) = 5x³ + 4x² - 3x + C

keterangan : Jika diintegralkan pangkat x akan naik satu dan dikalikan seper pangkat barunya. Jika ada angka diintegralkan menjadi ada x nya misal -3 diintegralkan menjadi -3x. Pada akhir pengitegralan selalu ditulis ditambah C. "C" merupakan suatu konstanta/angka yang nilainya tidak dapat ditentukan.

Coba perhatikan....

pada awalnya f (x) = 5x³ + 4x² - 3x + 7 setelah dirurunkan menjadi f ' (x) = 15x² + 8x - 3.
kemudian f ' (x) diintegralkan menjadi f (x) = 5x³ + 4x² - 3x + C. Jika diperhatikan angka koefisien f (x) yakni 7 setelah diturunkan dan menjadi nol ( 0 ) saat diintegralkan kembali tidak dapat ditentukan dan ditulis dengan lambang C.

untuk mencari nilai C diperlukan keterangan tambahan.....

misal : f (1) = 13 berarti 5.1³ + 4.1² - 3.1+ C = 13 maka C = 13 - 9 =7

fungsi f (x) = 5x³ + 4x² - 3x + 7

Soal-soal integral sangat berkaitan dengan bentuk2 perpangkatan (materi kelas X bab I). Jadi yang masih bingung bentuk perpangkatan harus dipelajari dulu...

Contoh soal integral lainnya :

$\begin{align*}1.\;\;\int {\color{Blue} 3}x^{\color{Red} 2}dx&=&\frac{{\color{Blue} 3}}{{\color{Red} 2}+1}\;x^{{\color{Red} 2}+1}+C\\&=&x^3\;\;+\;C \end{align*}$

$\begin{align*}2.\;\;\int \sqrt{x}\;dx&=&\int x^{\frac 12}\;dx\\&=&\frac{1}{\frac 12+1}\;x^{\frac 12+1}+C\\&=&\frac{\;\;1\;\;}{\frac 32}\;x^{\frac 32}+C\\&=&\frac 23\;x\sqrt{x}+C \end{align*}$

$\begin{align*}3.\;\;\int \frac{{\color{Blue} 3}}{x^{\color{Red} 2}}\;dx&=& \int {\color{Blue} 3}.x^{{\color{Red} -2}}\;dx\\&=&\frac{{\color{Blue} 3}}{{\color{Red} -2}+1}x^{-2+1}\;+C\\&=&\frac{3}{-1}\;x^{-1}+C\\&=&-\frac{3}{x}\;+\;C\end{align*}$

Perhatikan untuk contoh no.2 dan no.3 fungsi f(x) dinyatakan terlebih dulu sebagai fungsi pangkat,yaa…..jangan sampai terlupa !!!

Lanjut ke soal lainnya....

1. Tentukan integral dari $f(x)=5x^4+\frac{2\pi}{3}$ !
Jawab :

$\begin{align*} \int f(x)\;dx&=&\int {\color{Red} 5}x^{\color{Red} 4}+{\color{Blue} \frac{2\pi}{3}}\;dx\\&=&\frac{{\color{Blue} 5}}{{\color{Red} 4}+1}\;x^{{\color{Red} 4}+1}+{\color{Blue} \frac{2\pi}{3}}\;x^{{\color{Red} 0}+1}+C\\&=&x^5+\frac{2\pi}{3}\;x+C\end{align*}$

2. Jika $f(x)=\int 3x^2-2x+6\;dx$ dan f(0)=-6

maka

Jawab :

$\begin{align*}f(x)&=&\int {\color{Blue} 3}x^{\color{Red} 2}-{\color{Blue} 2}x+{\color{Blue} 6}\;dx\\&=&\frac{{\color{Blue} 3}}{{\color{Red} 2}+1}\;x^{{\color{Red} 2}+1}-\frac{{\color{Blue} 2}}{{\color{Red} 1}+1}\;x^{{\color{Red} 1}+1}+\frac{{\color{Blue} 6}}{{\color{Red} 0}+1}x^{{\color{Red} 0}+1}+C\\f(x)&=&x^3-x^2+6x+C\end{align*}$

* Nah, karena f(0)=-6

maka kita bisa mencari C

$\begin{align*}f(x)&=&x^3-x^2+6x+C\\f(0)&=&0^3-0^2+6.0+C\\-6&=&C\end{align*}$

* Sehingga f(x)=x^3-x^2+6x+6

3. Tentukan integral dari $f(x)=\frac{6}{x^3}\;-\;\frac{3}{x^2}$ !!!
Jawab :

Ingat …. nyatakan dalam bentuk perpangkatan terlebih dulu tiap sukunya !!!

$\begin{align*}\int f(x)dx&=&\int \frac{{\color{Blue} 6}}{x^{\color{Red} 3}}\;-\;\frac{{\color{Blue} 3}}{x^{\color{Red} 2}}\;dx\\&=&\int {\color{Blue} 6}.x^{{\color{Red} -3}}-{\color{Blue} 3}.x^{{\color{Red} -2}}\;dx\\&=&\frac{{\color{Blue} 6}}{{\color{Red} -3}+1}\;x^{{\color{Red} -3}+1}-\frac{{\color{Blue} 3}}{{\color{Red} -2}+1}\;x^{{\color{Red} -2}+1}+C\\&=&-3x^{-2}-(-3)x^{-1}+C\\&=&-\frac{3}{x^2}+\frac 3x+C\end{align*}$

4. Tentukan integral dari $f(x)=2\sqrt x+3x\sqrt x$ !!!!

Jawab:

* Ingat …. nyatakan dalam bentuk perpangkatan terlebih dulu tiap sukunya !!!

$\begin{align*}\int f(x)dx&=&\int 2\sqrt x+3x\sqrt x\;dx\\&=&\int {\color{Blue} 2}.x^{{\color{Red} \frac 12}}+{\color{Blue} 3}.x^{{\color{Red} \frac 32}}\;dx\\&=&\frac{{\color{Blue} 2}}{{\color{Red} \frac 12}+1}\;x^{{\color{Red} \frac 12}+1}+\frac{{\color{Blue} 3}}{{\color{Red} \frac 32}+1}\;x^{{\color{Red} \frac 32}+1}+C\\&=&\frac{\;2\;}{\frac 32}x^{\frac 32}+\frac{\;3\;}{\frac 52}x^{\frac 52}+C\\&=&2.\frac 23\;x^{\frac 32}+3.\frac 25\;x^{\frac 52}+C\\&=&\frac 43\;x\sqrt x+\frac 65\;x^2\sqrt x+C \end{align*}$

ayooo silahkan dicoba dengan soal-soal yang lain ya….

Sifat -sifat :

$\int kf(x)\;dx=k\int f(x)\;dx$

$\int f(x)+g(x)\;dx=\int f(x)\;dx+\int g(x)dx$

$\int f(x)-g(x)\;dx=\int f(x)\;dx-\int g(x)\;dx$

Keterangan di atas arti mudahnya... diartikan jika ada bentuk penjumlahan atau pengurangan dalam soal integral maka dapat diintegralkan sendiri2.....misalnya soal ini :

$\int\frac{x^3-1}{\sqrt x}dx$ adalah…

a. $\frac 27.\sqrt x(x^3-7) +c$

b. $\frac 27.\sqrt x(x^3+7) +c$

c. $\frac 17.\sqrt x(x^3+7) +c$

d. $\frac 17.\sqrt x(x^3-7) +c$

e. $\frac 27.\sqrt x(x^3+1) +c$

Jawab:

$\int\frac{x^3-1}{\sqrt x}dx$ karena penyebut satu suku,maka pisahkan fungsi pembilangnya :

$\dpi{100} \bg_white \begin{align*}\int\frac{x^3-1}{\sqrt x}dx & = &\int(\frac{x^3}{\sqrt x} - \frac{1}{\sqrt x})dx\\ & = &\int \frac{x^3}{x^{\frac 12}}dx - \int\frac{1}{x^{\frac 12}}dx\\ & = &\int x^{\frac 52}dx - \int x^{-\frac 12}dx\\ & = &\frac{1}{\frac 52+1}.x^{\frac 52+1} - \frac{1}{-\frac 12+1}.x^{-\frac 12+1}+c\\ & = &\frac{1}{\frac 72}.x^{\frac 72} - \frac{1}{\frac 12}.x^{\frac 12}+c\\ & = &\frac 27.x^{\frac 72} - 2x^{\frac 12}+c\\ & = &\frac 27.x^3.\sqrt x-2.\sqrt x+c\\ & = &\frac{2}{7}\sqrt x (x^3-7)+c\end{align*}$

TEKNIK MESIN 45-NABHAN

Thursday, May 31, 2012

Integral

Integral

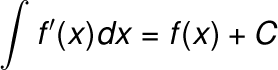
No comments:

Post a Comment

Search This Blog